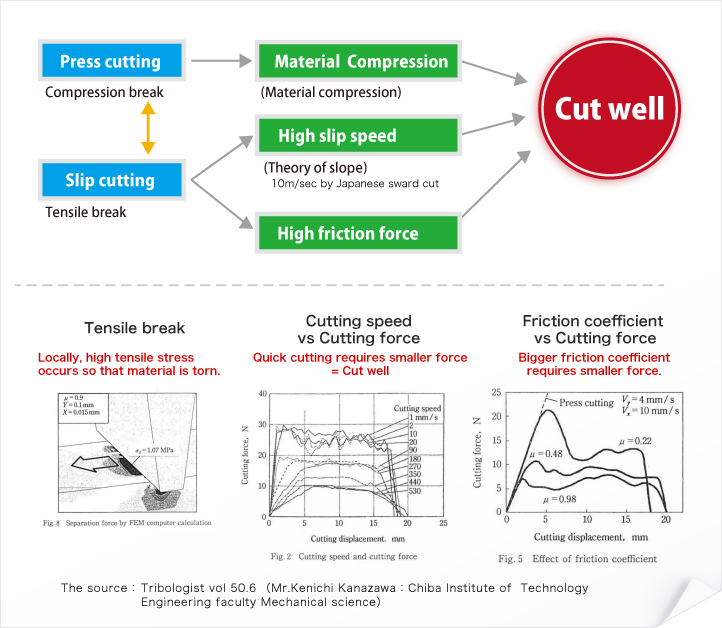
Looking Good Tips About What Is The V Cut Theory Romantic Updo Hairstyles For Long Hair

De nition 1 (directed graph).

What is the v cut theory. Let 'g' be a connected graph. Produced by rob szypko , sydney harper , stella tan , asthaa chaturvedi and rachelle bonja. Then the cut induced by this partition is formally defined as the set of all the edges.

Given s;t2v, an (s;t) cut is a cut s.t. In other words, a cut set is a set of edges that, if removed, will separate the graph into. If {v1, v2} is a partition of v, the set e(v1, v2) of all.

In graph theory, a cut is a partition of the vertices of a graph into two disjoint subsets. In graph theory, a cut set is a set of edges in a graph that, if removed, will disconnect the graph. To quote from reinhard diestel's graduate textbook on graph theory, the definition of a cut is very simple:

Furthermore, we’ll present several examples of cut and also discuss the. In a flow network, the source is located in s, and the sink is located in t. S2s;t2s a cut set of a cut is (u;v) :

China’s expansion and russia’s threats of using nuclear weapons in ukraine and in space have changed a u.s. Drive to reduce nuclear weapons. Case, it makes sense to say that v is a cut vertex if g − v has more connected components than g.

In this tutorial, we’ll discuss the cut property in a minimum spanning tree. Define given g= (v;e), a cut is a partition of v, (s;s ), where sˆv. A cut is a partition of the vertices into disjoint subsets s and t.

This type of subgraph is known as cut set of g. In graph theory, a cut is a partition of the vertices of a graph into two disjoint subsets. A vertex v of a connected graph g is a cut vertex of g if and only if there exist vertices u and w distinct from v such that there’s at least one u−w path in g and v lies on every.

Show that a vertex c in the connected simple graph g is a cut vertex if and only if there are vertices u and v, both different from c, such that every path between u and v passes. In graph theory, a cut is a partition of the vertices of a graph into two disjoint subsets. Edited by marc georges and lisa chow.

Flows and cuts graph theory (fall 2011) rutgers university swastik kopparty 1 flows we now study ows on graphs. Let’s see how this helps us break a problem down into. These edges are said to cross the cut.

Given a graph $g$ with vertex set $v$, let $u$ and $w$ form a partition of $v$. A vertex cut in a graph g is a subset u ⊆ v (g) such that g − u (that’s the subgraph of g with the vertices in u, and all their incident edges, deleted) is no longer connected. A directed graph gis a tuple.